일정한 간격으로
동일한 값이 반복 되는 것을
주기적이다 라고 합니다
삼각함수인 sin, cos, tan 는
주기적인 성질을 가지고 있고
그래서 주기함수 라고 하죠

주기함수의 개념을
이야기 하자면...
함수 y = f(x)의 정의역에 속하는
모든 x에 대해서
f(x+p) = f(x)를 만족시키는
0이 아닌 상수의 p가 존재하면
y=f(x)를 주기함수라고 하며
이때 상수 p 중에서
최소인 양수를
그 함수의 주기라고 합니다
<상수 p 주기 이해하기>
항상 느끼지만
개념은 설명을 해주기는 하는데
무슨 말을 하는지 모르겠네요
예시에 숫자를 넣어서
이해를 해봅시다

여기서 f(x) 의 주기는 몇 일까요?
2가 됩니다
왜?
f(x+p) = f(x) 를 만족하는
0이 아닌 상수 p가 존재하면
여기서 p가 주기라고 했었죠?
f(x+2) = f(x)는
p 자리에 숫자 2가 들어갔고
2는 0이 아니며 상수입니다
그렇다면 주기는?
네 그렇죠 2 입니다
<삼각함수 주기>
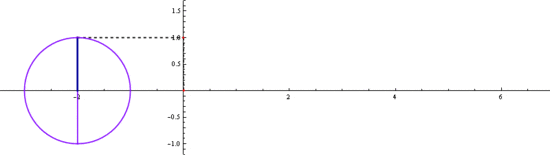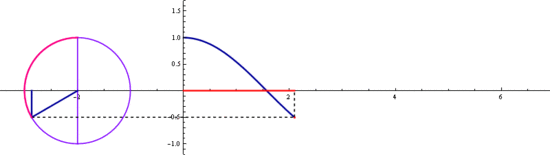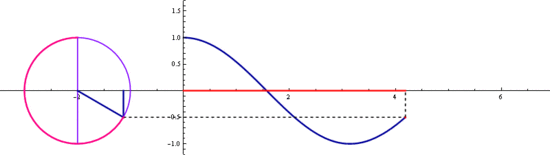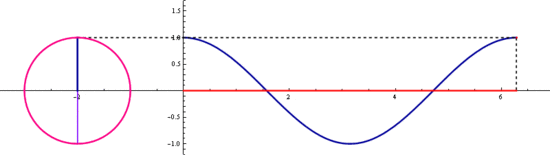
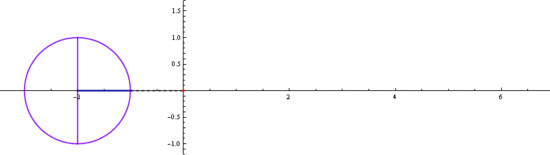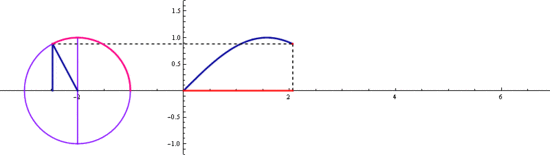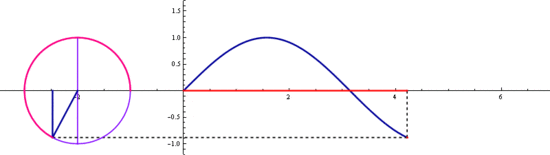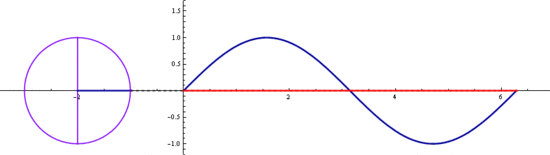
삼각함수 sin과 cos는
기본 주기가 2π 입니다
2π마다 같은 값이 반복되죠
tan은 기본 주기가 π 이고
π마다 같은 값이 반복됩니다
그런데 삼각함수가 변형되면
그에 따라서 주기도 변합니다
예를 들어서
y = a sin(bx + c) + d 의 경우
sin과 cos 함수의 주기는 2π / |b| 이고
tan 함수의 주기는 π / |b| 입니다
Q. 왜 그렇게 되는데요?
A. 식을 전개해보면 알 수 있습니다
sin(x)의 주기는 2π 이죠?
따라서 sin(x) = sin(x+2π) 입니다
( f(x+p) = f(x) ◀ 이거 기억하고 있죠??)
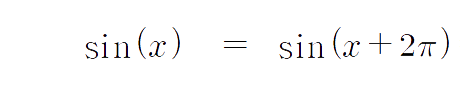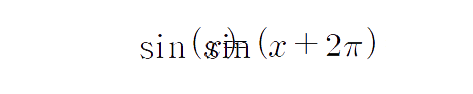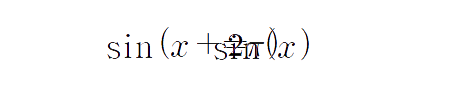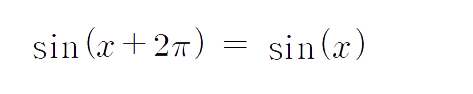
보기 편하게 양쪽을 바꿉시다
sin(x+2π) = sin(x)
y = a sin(bx + c) + d 는
x자리에 bx가 들어간 상황이죠?
sin(x+2π) = sin(x)
위의 식에도 x 자리에 bx를 넣어봅시다
그럼 sin(bx+2π) = sin(bx) 되는데
여기서 bx자리에 b(x+p)를 넣어도 됩니다
왜?
계속 나오지만
f(x+p) = f(x) 입니다
보기 쉽게 좌우를 바꿀까요?
f(x) = f(x+p)
귀찮으니 f()도 치우죠
x = x+p
이제 양쪽에 b를 곱해봅시다
b*x = b*(x+p)
곱하기 기호 *를 생략하면?
bx = b(x+p)
다시 원래 이야기로 돌아가서
sin(bx+2π) = sin(bx) 도
sin ( ) 를 치워봅시다
bx+2π = bx 가 되는데
bx = b(x+p) 였죠?
A = B 이고 B = C 라면
A = B = C 이기 때문에
A = C가 성립해야 합니다
bx+2π = bx = b(x+p) 이기 때문에
bx+2π = b(x+p)가 성립해야 하죠
b(x+p)를 전개하면?= bx+bp가 됩니다
bx+2π = bx+bp
양쪽에 bx가 있네요?
양쪽에 -bx를 해서 없애버립시다
2π = bp
이제 양쪽을 b로 나누면
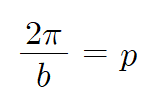
p는 뭐였죠?
네 주기 입니다
그래서 y = sin(bx) 의 주기는
2π / |b| 가 됩니다
<예제 문제>

주기 부터 계산해봅시다
x 앞에 있는 숫자가? 4 네요
(저기가 b 자리였었죠)
sin(4x)의 주기는?
2π / |4| = π / 2 입니다
최대값, 최소값은 쉽죠?
sin함수의 최대값은 1 이고
최솟값은 -1 이기 때문에
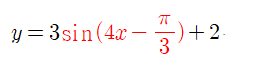
sin함수 자리에 1을 넣어서 계산하면 최대값
-1을 넣어서 계산하면 최소값 입니다
1을 넣으면?
y = 3 x 1 + 2
= 3 + 2
= 5
-1을 넣으면?
y = 3 x -1 + 2
= -3 + 2
= -1
최대값은 5
최소값은 -1